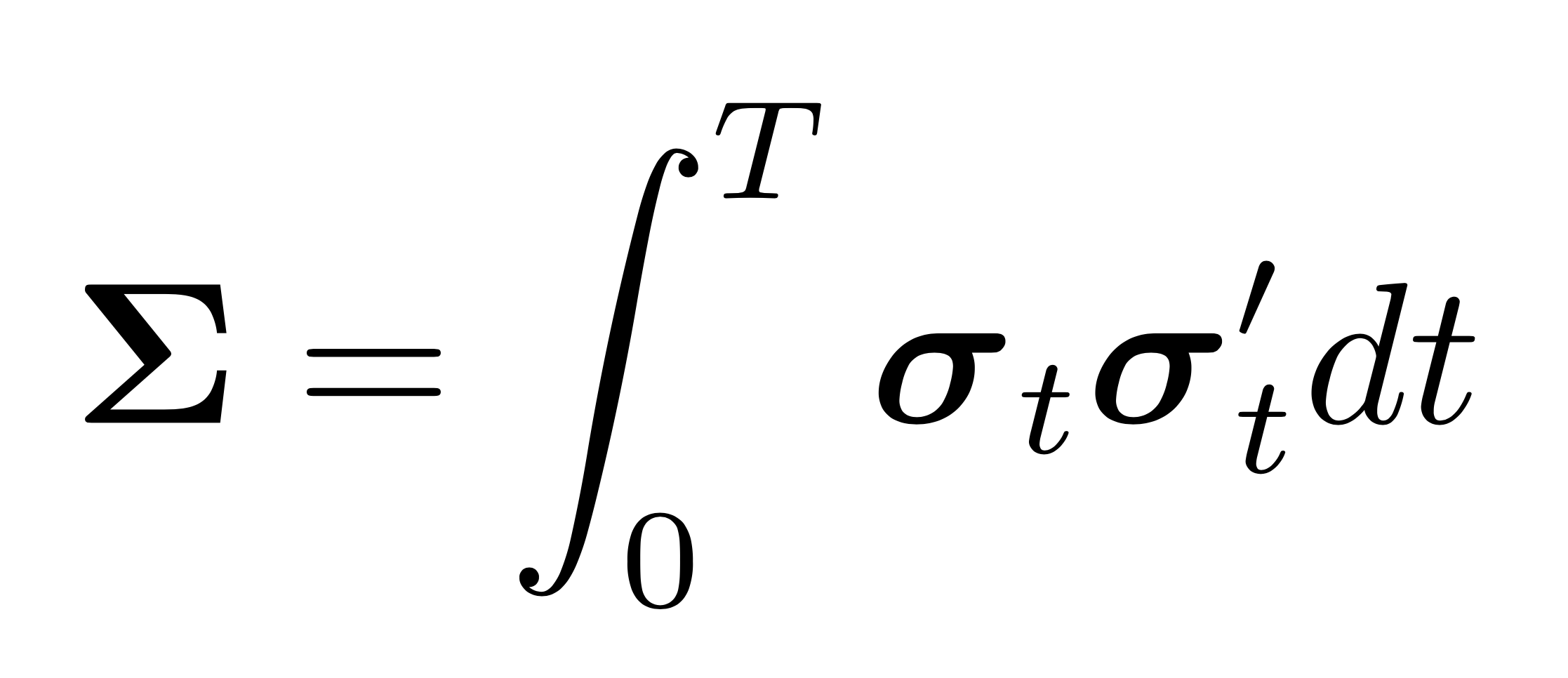nercome

hd.nercome(X, m=None, M=50)

The nonparametric eigenvalue-regularized covariance matrix estimator (NERCOME) of Lam (2016).

Parameters

Xnumpy.ndarray, shape = (p, n)

A 2d array of log-returns (n observations of p assets).

mint, default = None

The size of the random split with which the eigenvalues are computed. If None the estimator searches over values suggested by Lam (2016) in Equation (4.8) and selects the best according to Equation (4.7).

Mint, default = 50

The number of permutations. Lam (2016) suggests 50.

Returns

opt_Sigma_hatnumpy.ndarray, shape = (p, p)

The NERCOME covariance matrix estimate.

Notes

A very different approach to the analytic formulas of nonlinear shrinkage is pursued by Abadir et al 2014. These authors propose a nonparametric estimator based on a sample splitting scheme. They split the data into two pieces and exploit the independence of observations across the splits to regularize the eigenvalues. Lam (2016) builds on their results and proposes a nonparametric estimator that is asymptotically optimal even if the population covariance matrix \(\mathbf{\Sigma}\) has a factor structure. In the case of low-rank strong factor models, the assumption that each observation can be written as \(\mathbf{x}_{t} =\mathbf{\Sigma}^{1 / 2} \mathbf{z}_{t}\) for \(t=1, \ldots, n,\) where each \(\mathbf{z}_{t}\) is a \(p \times 1\) vector of independent and identically distributed random variables \(z_{i t}\), for \(i=1, \ldots, p,\) with zero-mean and unit variance, is violated since the covariance matrix is singular and its Cholesky decomposition does not exist. Both linear_shrinkage() and nonlinear_shrinkage() are build on this assumption are no longer optimal if it is not fulfilled. The proposed nonparametric eigenvalue-regularized covariance matrix estimator (NERCOME) starts by splitting the data into two pieces of size \(n_1\) and \(n_2 = n - n_1\). It is assumed that the observations are i.i.d with finite fourth moments such that the statistics computed in the different splits are likewise independent of each other. The sample covariance matrix of the first partition is defined as \(\mathbf{S}_{n_1}:= \mathbf{X}_{n_1}\mathbf{X}_{n_1}'/n_1\). Its spectral decomposition is given by \(\mathbf{S}_{n_1}=\mathbf{U}_{n_1} \mathbf{\Lambda}_{n_1} \mathbf{U}_{n_1}^{\prime},\) where \(\mathbf{\Lambda}_{n_1}\) is a diagonal matrix, whose elements are the eigenvalues \(\mathbf{\lambda}_{n_1}=\left(\lambda_{n_1, 1}, \ldots, \lambda_{n_1, p}\right)\) and an orthogonal matrix \(\mathbf{U}_{n_1}\), whose columns \(\left[\mathbf{u}_{n_1, 1} \ldots \mathbf{u}_{n_1, p}\right]\) are the corresponding eigenvectors. Analogously, the sample covariance matrix of the second partition is defined by \(\mathbf{S}_{n_2}:= \mathbf{X}_{n_2}\mathbf{X}_{n_2}'/n_2\). Theorem 1 of Lam (2016) shows that \begin{equation} \widetilde{\mathbf{d}}_{n_1}^{(\text{NERCOME})}= \operatorname{diag}( \mathbf{U}_{n_1}^{\prime} \mathbf{S}_{n_2} \mathbf{U}_{n_1}) \end{equation} is asymptotically the same as the finite-sample optimal rotation equivariant \(\mathbf{d}_{n_1}^{*} = \mathbf{U}_{n_1}^{\prime} \mathbf{\Sigma} \mathbf{U}_{n_1}\) based on the section \(n_1\). The proposed estimator is thus of the rotation equivariant form, where the elements of the diagonal matrix are chosen according to \(\widetilde{\mathbf{d}}_{n_1}^{(\text{NERCOME})}\). In other words the estimator is given by \begin{equation} \widetilde{\mathbf{S}}_{ n_1}^{(\text{NERCOME})}:= \sum_{i=1}^{p}\widetilde{\mathbf{d}}_{n_1}^{(\text{NERCOME})} \cdot \mathbf{u}_{n_1, i} \mathbf{u}_{n_1, i}^{\prime} \end{equation} The author shows that this estimator is asymptotically optimal with respect to the Frobenius loss even under factor structure. However, it uses the sample data inefficiently since only one section is utilized for the calculation of each component. The natural extension is to permute the data and bisect it anew. With these sections an estimate is computed according to \(\widetilde{\mathbf{S}}_{ n_1}^{(\text{NERCOME})}\). This is done \(M\) times and the covariance matrix estimates are averaged: \begin{equation} \widetilde{\mathbf{S}}_{n_1, M}^{(\text{NERCOME})}:=\frac{1}{M} \sum_{j=1}^{M}\widetilde{\mathbf{S}}_{n_1, j}^{(\text{NERCOME})}. \end{equation} The estimator depends on two tuning parameters, \(M\) and \(n_1\). Higher \(M\) give more accurate results but the computational cost grows as well. The author suggests that more than 50 iterations are generally not needed for satisfactory results. \(n_1\) is subject to regularity conditions. The author proposes to search over the contenders \begin{equation} n_1=\left[2 n^{1 / 2}, 0.2 n, 0.4 n, 0.6 n, 0.8 n, n-2.5 n^{1 / 2}, n-1.5 n^{1 / 2}\right] \end{equation} and select the one that minimizes the following criterion inspired by Bickel (2008) \begin{equation} g(n_1)=\left\|\frac{1}{M} \sum_{j=1}^{M} \left(\widetilde{\mathbf{S}}_{n_1, j}^{(\text{NERCOME})} -\mathbf{S}_{n_2, j}\right)\right\|_{F}^{2}. \end{equation}

References

Abadir, K. M., Distaso, W. and Zikeˇs, F. (2014). Design-free estimation of variance matrices, Journal of Econometrics 181(2): 165–180.

Bickel, P. J. and Levina, E. (2008). Regularized estimation of large covariance matrices, The Annals of Statistics 36(1): 199–227.

Lam, C. (2016). Nonparametric eigenvalue-regularized precision or covariance matrix estimator, The Annals of Statistics 44(3): 928–953.

Examples

>>> np.random.seed(0)
>>> n = 13
>>> p = 5
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> cov = nercome(X.T, m=5, M=10)
>>> cov
array([[ 1.34226722,  0.09693429,  0.00233125,  0.17717658, -0.01643898],
       [ 0.09693429,  1.0508423 ,  0.10112215, -0.22908987, -0.04914651],
       [ 0.00233125,  0.10112215,  1.0731665 , -0.02959628,  0.38652859],
       [ 0.17717658, -0.22908987, -0.02959628,  1.10753766,  0.1807373 ],
       [-0.01643898, -0.04914651,  0.38652859,  0.1807373 ,  0.88832791]])