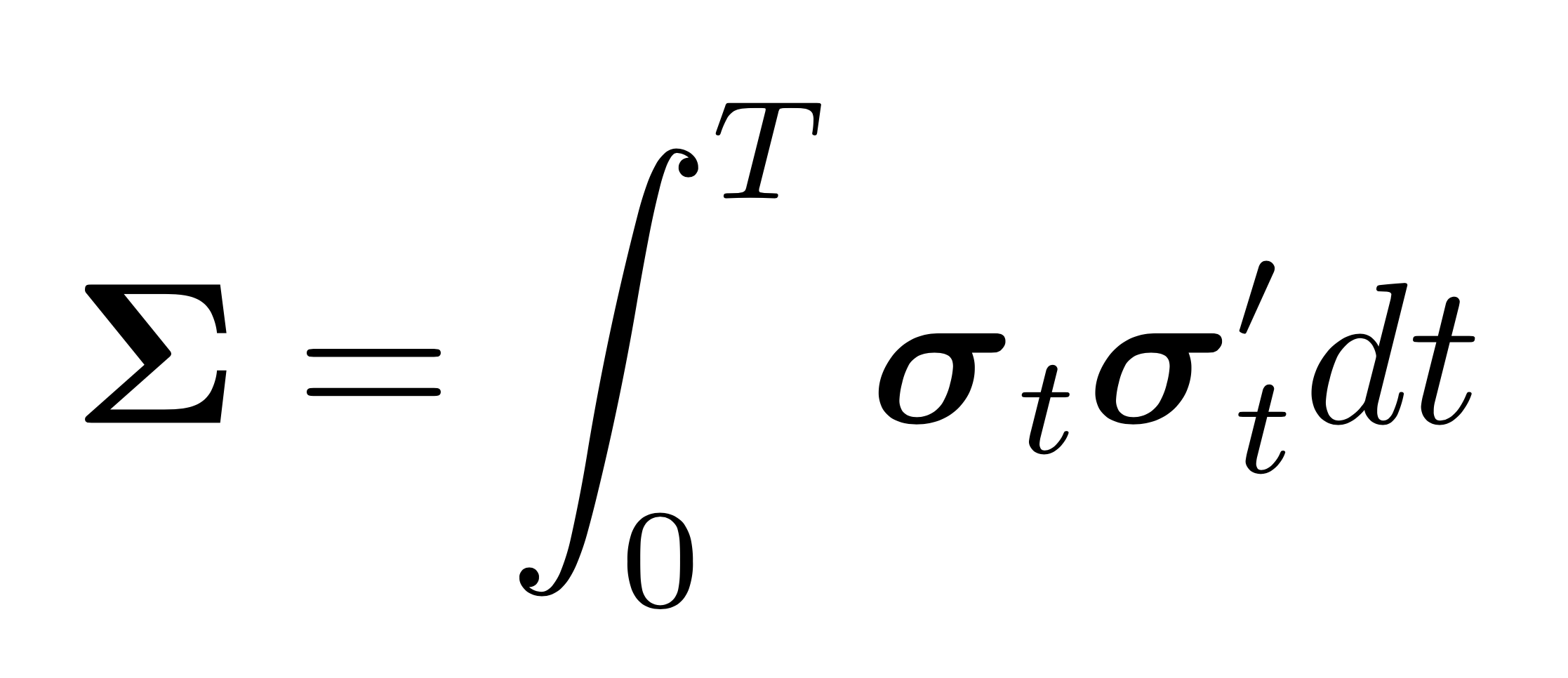"""This module provides functions to estimate covariance matrices in
high dimension, i.e., when the concentration ratio is not small or even greater
than one. """
import numpy as np
import warnings
import numba
from hfhd import hf
import datetime
[docs]def fsopt(S, sigma):
r"""
The infeasible finite sample optimal rotation equivariant covariance
matrix estimator of Ledoit and Wolf (2018).
Parameters
----------
S : numpy.ndarray
The sample covariance matrix.
sigma : numpy.ndarray
The (true) population covariance matrix.
Returns
-------
out : numpy.ndarray
The finite sample optimal rotation equivariant covariance
matrix estimate.
Notes
-----
This estimator is given by
.. math::
S_{n}^{*}:=\sum_{i=1}^{p} d_{n, i}^{*} \cdot u_{n, i} u_{n, i}^{\prime}
=\sum_{i=1}^{p}\left(u_{n, i}^{\prime}
\Sigma_{n} u_{n, i}\right) \cdot u_{n, i} u_{n, i}^{\prime},
where $\left[u_{n, 1} \ldots u_{n, p}\right]$ are the sample eigenvectors.
References
----------
Ledoit, O. and Wolf, M. (2018).
Analytical nonlinear shrinkage of large-dimensional covariance matrices,
University of Zurich, Department of Economics, Working Paper (264).
"""
lambd, u = np.linalg.eigh(S)
d = np.einsum("ji, jk, ki -> i", u, sigma, u)
return u @ np.diag(d) @ u.T
[docs]def linear_shrinkage(X):
r"""
The linear shrinkage estimator of Ledoit and Wolf (2004). The
observations need to be synchronized and i.i.d.
Parameters
----------
X : numpy.ndarray, shape = (p, n)
A sample of synchronized log-returns.
Returns
-------
shrunk_cov : numpy.ndarray
The linearly shrunk covariance matrix.
Examples
--------
>>> np.random.seed(0)
>>> n = 5
>>> p = 5
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> cov = linear_shrinkage(X.T)
>>> cov
array([[1.1996234, 0. , 0. , 0. , 0. ],
[0. , 1.1996234, 0. , 0. , 0. ],
[0. , 0. , 1.1996234, 0. , 0. ],
[0. , 0. , 0. , 1.1996234, 0. ],
[0. , 0. , 0. , 0. , 1.1996234]])
Notes
-----
The most ubiquitous estimator of the rotation equivariant type is perhaps
the linear shrinkage estimator of Ledoit and Wolf (2004). These authors
propose a weighted average of the sample covariance matrix and the identity
(or some other highly structured) matrix that is scaled such that the trace
remains the same. The weight, or shrinkage intensity, $\rho$ is chosen such
that the squared Frobenius loss is minimized by inducing bias but reducing
variance. In Theorem 1, the authors show that the optimal $\rho$ is given by
\begin{equation}
\rho=\beta^{2} /\left(\alpha^{2}+\beta^{2}\right)=\beta^{2} / \delta^{2},
\end{equation}
where $\mu=\operatorname{tr}(\mathbf{\Sigma})/p$, $\alpha^{2}=
\|\mathbf{\Sigma}-\mu \mathbf{I}_p\|_{F}^{2}$, $\beta^{2}=
E\left[\|\mathbf{S}-\mathbf{\Sigma}\|_{F}^{2}\right]$,
and $\delta^{2}=E\left[\|\mathbf{S}-\mu \mathbf{I}_p\|_{F}^{2}\right]$.
$\beta^{2} / \delta^{2}$ can be interpreted as a normalized measure of the
error of the sample covariance matrix.
Shrinking the covariance matrix towards the $\mu$-scaled identity matrix
has the effect of pulling the eigenvalues towards $\mu$. This reduces
eigenvalue dispersion.
In other words, the elements of the diagonal matrix in the rotation
equivariant form are chosen as
\begin{equation}
\widehat{\mathbf{\delta}}^{(l, o)}:=\left(\widehat{d}_{1}^{(l, o)},
\ldots, \widehat{d}_{p}^{(l, o)}\right)=\left(\rho \mu+(1-\rho)
\lambda_{1}, \ldots, \rho \mu+(1-\rho) \lambda_{p}\right).
\end{equation}
In the current form it is still an oracle estimator since it depends on ]
unobservable quantities.
To make it a feasible estimator, these quantities have to be estimated. To
this end, define the grand mean as
\begin{equation}
\label{eqn: grand mean}
\bar{\lambda}:=\frac{1}{p} \sum_{i=1}^{p} \lambda_{i},
\end{equation}
The estimator for $\rho$ is given by
\begin{equation}
\widehat{\rho} : = \frac{b^{2}}{d^{2}},
\end{equation}
where $d^{2}=\left\|\mathbf{S}-\bar{\lambda} \mathbf{I}_{p}
\right\|_{F}^{2}$ and $b^{2}=\min \left(\bar{b}^{2}, d^{2}\right)$ with
$\bar{b}^{2}=\frac{1}{n^{2}} \sum_{k=1}^{n}\left\|\mathbf{x}_{k}
\left(\mathbf{x}_{k}\right)^{\prime}-\mathbf{S}\right\|_{F}^{2}$,
where $\mathbf{x}_{k}$ denotes the $k$th column of the observation
matrix $\mathbf{X}$ for $k=1, \ldots, n$. In order for this estimator
to be consistent, the assumption that $\mathbf{X}$ is i.i.d with finite
fourth moments must be satisfied. The feasible linear shrinkage estimator
is then of form rotation equivatiant form with the elements of the diagonal
chosen as
\begin{equation}
\widehat{\mathbf{\delta}}^{(l)}:=\left(\widehat{d}_{{1}}^{(l)}, \ldots,
\widehat{d}_{p}^{(l)}\right)=\left( \widehat{\rho} \bar{\lambda}+
(1- \widehat{\rho}) \lambda_{1}, \ldots, \widehat{\rho} \bar{\lambda}+
(1- \widehat{\rho}) \lambda_{p}\right).
\end{equation}
Hence, the linear shrinkage estimator is given by
\begin{equation}
\widehat{\mathbf{S}}:=\sum_{i=1}^{p} \widehat{d}_{i}^{(l)}
\mathbf{u}_{i} \mathbf{u}_{i}^{\prime}
\end{equation}
The result is a biased but well-conditioned covariance matrix estimate.
References
----------
Ledoit, O. and Wolf, M. (2004).
A well-conditioned estimator for large-dimensional covariance matrices,
Journal of Multivariate Analysis 88(2): 365–411.
"""
S = np.cov(X)
rho_hat = _linear_shrinkage_intensity(X, S)
shrunk_cov = _linear_shrinkage_cov(S, rho_hat)
return shrunk_cov
def _linear_shrinkage_cov(S, rho=0.1):
"""
Linearly shrink a sample covariance matrix with shrinkage intensity
``rho``.
Parameters
----------
S : numpy.ndarray, shape = (p, p)
The sample covariance matrix.
rho : float, 0 <= rho <= 1
The shrinkage intensity.
Returns
-------
shrunk_cov : numpy.ndarray
The shrunk covariance matrix.
Examples
--------
>>> np.random.seed(0)
>>> n = 5
>>> p = 5
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> S = np.cov(X.T)
>>> cov = _linear_shrinkage_cov(S, 0.1)
>>> cov
array([[ 2.45653147, 0.02090578, 0.06479169, 1.47201982, -0.46265304],
[ 0.02090578, 0.32973086, -0.13795285, -0.1922658 , -0.47424349],
[ 0.06479169, -0.13795285, 0.42122102, 0.17390622, 0.535665 ],
[ 1.47201982, -0.1922658 , 0.17390622, 1.25079368, 0.16427303],
[-0.46265304, -0.47424349, 0.535665 , 0.16427303, 1.53983998]])
"""
p = S.shape[0]
lambda_bar = np.trace(S) / p
shrunk_cov = rho * lambda_bar * np.eye(p) + (1 - rho) * S
return shrunk_cov
def _linear_shrinkage_intensity(X, S):
"""
Compute the optimal linear shrinkage intensity given a sample and a
covariance matrix estimate according to Ledoit and Wolf (2004).
Parameters
----------
X : numpy.ndarray, shape = (p, n)
A sample of synchronized log-returns.
S : numpy.ndarray, shape = (p, p)
A sample covariance matrix of synchronized log-returns.
Returns
-------
rho_hat : numpy.ndarray
The estimate of the optimal linear shrinkage intensity.
Notes
-----
Assumption: independent and identically distributed
observations with finite fourth moments.
"""
p, n = X.shape
evalues = np.linalg.eigvalsh(S)
lambd = np.mean(evalues)
temp = [np.linalg.norm(np.outer(X[:, i], X[:, i]) - S, 'fro')**2
for i in range(n)]
b_bar_sq = np.sum(temp)/n**2
d_sq = np.linalg.norm(S - lambd*np.eye(p), 'fro')**2
b_sq = np.minimum(b_bar_sq, d_sq)
rho_hat = b_sq/d_sq
return rho_hat
[docs]def linear_shrink_target(cov, target, step=0.05, max_iter=100):
r"""
Linearly shrink a covariance matrix until a condition number target is
reached. Useful for reducing the impact of outliers in :func:`nerive`.
Parameters
----------
cov : numpy.ndarray, shape = (p, p)
The covariance matrix.
target: float > 1
The highest acceptable condition number.
step : float > 0
The linear shrinkage parameter for each step.
max_iter : int > 1
The maximum number of iterations until giving up.
Returns
-------
cov : numpy.ndarray, shape = (p, p)
The linearly shrunk covariance matrix estimate.
"""
assert target > 1, "Target cond must be greater 1."
for _ in range(max_iter):
cond = np.linalg.cond(cov)
if cond <= target:
break
cov = _linear_shrinkage_cov(cov, step)
return cov
[docs]def nonlinear_shrinkage(X):
r"""
Compute the shrunk sample covariance matrix with the analytic nonlinear
shrinkage formula of Ledoit and Wolf (2018). This estimator shrinks the
sample sample covariance matrix with :func:`~_nonlinear_shrinkage_cov`.
The code has been adapted from the Matlab implementation provided by the
authors in Appendix D.
Parameters
----------
x : numpy.ndarray, shape = (p, n)
A sample of synchronized log-returns.
Returns
-------
sigmatilde : numpy.ndarray, shape = (p, p)
The nonlinearly shrunk covariance matrix estimate.
Examples
--------
>>> np.random.seed(0)
>>> n = 13
>>> p = 6
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> nonlinear_shrinkage(X.T)
array([[ 1.50231589e+00, -2.49140874e-01, 2.68050353e-01,
2.69052962e-01, 3.42958216e-01, -1.51487901e-02],
[-2.49140874e-01, 1.05011440e+00, -1.20681859e-03,
-1.25414579e-01, -1.81604754e-01, 4.38535891e-02],
[ 2.68050353e-01, -1.20681859e-03, 1.02797073e+00,
1.19235516e-01, 1.03335603e-01, 8.58533018e-02],
[ 2.69052962e-01, -1.25414579e-01, 1.19235516e-01,
1.03290514e+00, 2.18096913e-01, 5.63011351e-02],
[ 3.42958216e-01, -1.81604754e-01, 1.03335603e-01,
2.18096913e-01, 1.22086494e+00, 1.07255380e-01],
[-1.51487901e-02, 4.38535891e-02, 8.58533018e-02,
5.63011351e-02, 1.07255380e-01, 1.07710975e+00]])
Notes
-----
The idea of shrinkage covariance estimators is further developed by
Ledoit and Wolf (2012) who argue that given a sample of size
$\mathcal{O}(p^2)$, estimating $\mathcal{O}(1)$ parameters, as in linear
shrinkage, is precise but too restrictive, while estimating
$\mathcal{O}(p^2)$ parameters, as in the the sample covariance matrix,
is impossible. They argue that the optimal number of parameters to estimate
is $\mathcal{O}(p)$. Their proposed non-linear shrinkage estimator uses
exactly $p$ parameters, one for each eigenvalue, to regularize each
eigenvalue with a specific shrinkage intensity individually. Linear
shrinkage, in contrast, is restricted by a single shrinkage intensity
with which all eigenvalues are shrunk uniformly. Nonlinear shrinkage
enables a nonlinear fit of the shrunk eigenvalues, which is appropriate
when there are clusters of eigenvalues. In this case, it may be optimal to
pull a small eigenvalue (i.e., an eigenvalue that is below the grand mean)
further downwards and hence further away from the grand mean. Linear
shrinkage, in contrast, always pulls a small eigenvalue upwards.
Ledoit and Wolf (2018) find an analytic formula based on the Hilbert
transform that nonlinearly shrinks eigenvalues asymptotically optimally
with respect to the MV-loss function (as well as the quadratic Frobenius
loss). The shrinkage function via the Hilbert transform can be interpreted
as a local attractor. Much like the gravitational field extended into
space by massive objects, eigenvalue clusters exert an attraction force
that increases with the mass (i.e. the number of eigenvalues in the
cluster) and decreases with the distance. If an eigenvalue
$\lambda_i$ has many neighboring eigenvalues slightly smaller than itself,
the exerted force on $\lambda_i$ will have large magnitude and downward
direction. If $\lambda_i$ has many neighboring eigenvalues slightly
larger than itself, the exerted force on $\lambda_i$ will also have
large magnitude but upward direction. If the neighboring eigenvalues
are much larger or much smaller than $\lambda_i$ the magnitude of the
force on $\lambda_i$ will be small. The nonlinear effect this has on the
shrunk eigenvalues can be seen in the figure below. The linearly shrunk
eigenvalues, on the other hand, follow a line. Both approaches reduce the
dispersion of eigenvalues and hence deserve the name shrinkage.
.. image:: ../img/nls_fit.png
The authors assume that there exists a $n \times p$ matrix
$\mathbf{Z}$ of i.i.d. random variables with mean zero, variance one,
and finite 16th moment such that the matrix of
observations $\mathbf{X}:=\mathbf{Z} \mathbf{\Sigma}^{1/2}$.
Neither $\mathbf{\Sigma}^{1/2}$ nor
$\mathbf{Z}$ are observed on their own. This assumption might not be
satisfied if the data generating process is a factor model. Use
:func:`~nercome` or :func:`~nerive` if you believe the assumption is
in your dataset violated.
Theorem 3.1 of Ledoit and Wolf (2018) states that under their assumptions
and general asymptotics the MV-loss is minimized by a rotation equivariant
covariance estimator, where the elements of the diagonal matrix are
\begin{equation}
\label{eqn: oracle diag}
\widehat{\mathbf{\delta}}^{(o, nl)}:=\left(\widehat{d}_{1}^{(o, nl)},
\ldots, \widetilde{d}_{p}^{(o, nl)}\right):=\left(d^{(o, nl)}\left(
\lambda_{1}\right), \ldots, d^{(o, nl)}\left(\lambda_{p}\right)\right).
\end{equation}
$d^{(o, nl)}(x)$ denotes the oracle nonlinear shrinkage function and it is
defined as
\begin{equation}
\forall x \in \operatorname{Supp}(F) \quad d^{(o, nl)}(x):=\frac{x}{
[\pi c x f(x)]^{2}+\left[1-c-\pi c x \mathcal{H}_{f}(x)\right]^{2}},
\end{equation}
where $\mathcal{H}_{g}(x)$ is the Hilbert transform. As per Definition 2
of Ledoit and Wolf (2018) it is defined as
\begin{equation}
\forall x \in \mathbb{R} \quad \mathcal{H}_{g}(x):=\frac{1}{\pi} P V
\int_{-\infty}^{+\infty} g(t) \frac{d t}{t-x},
\end{equation}
which uses the Cauchy Principal Value, denoted as $PV$ to evaluate the
singular integral in the following way
\begin{equation}
P V \int_{-\infty}^{+\infty} g(t) \frac{d t}{t-x}:=\lim _{\varepsilon
\rightarrow 0^{+}}\left[\int_{-\infty}^{x-\varepsilon} g(t) \frac{d t}
{t-x}+\int_{x+\varepsilon}^{+\infty} g(t) \frac{d t}{t-x}\right].
\end{equation}
It is an oracle estimator due to the dependence on the limiting sample
spectral density $f$, its Hilbert transform $\mathcal{H}_f$, and the
limiting concentration ratio $c$, which are all unobservable. Nevertheless,
it represents progress compared to
:func:`hd.fsopt`, since it no longer depends on the full population
covariance matrix, $\mathbf{\Sigma}$, but only on its eigenvalues.
This reduces the number of parameters to be estimated from the impossible
$\mathcal{O}(p^2)$ to the manageable $\mathcal{O}(p)$. To make the
estimator feasible, unobserved quantities have to be replaced by statistics.
A consistent estimator for the limiting concentration $c$ is the sample
concentration $c_n = p/n$. For the limiting sample spectral density $f$,
the authors propose a kernel estimator. This is necessary, even though
$F_{n}\stackrel{\text { a.s }}{\rightarrow} F$, since $F_n$ is
discontinuous at every $\lambda_{i}$ and thus its derivative $f_n$, which
would've been the natural estimator for $f$, does not exist there. A
kernel density estimator is a non-parametric estimator of the probability
density function of a random variable. In kernel density estimation data
from a finite sample is smoothed with a non-negative function $K$, called
the kernel, and a smoothing parameter $h$, called the bandwidth, to make
inferences about the population density. A kernel estimator is of the form
\begin{equation}
\widehat{f}_{h}(x)=\frac{1}{N} \sum_{i=1}^{N} K_{h}\left(x-x_{i}\right)=
\frac{1}{N h} \sum_{i=1}^{N} K\left(\frac{x-x_{i}}{h}\right).
\end{equation}
The chosen kernel estimator for the limiting sample spectral density is
based on the Epanechnikov kernel with a variable bandwidth, proportional
to the eigenvalues, $h_{i}:=\lambda_{i} h,$ for $i=1, \ldots, p$, where
the global bandwidth is set to $h:=n^{-1 / 3}$. The reasoning behind the
variable bandwidth choice can be intuited from the figure below,
which shows that the support of the limiting sample spectral distribution is
approximately proportional to the eigenvalue.
.. image:: ../img/lssd.png
The Epanechnikov kernel is defined as
\begin{equation}
\forall x \in \mathbb{R} \quad \kappa^{(E)}(x):=
\frac{3}{4 \sqrt{5}}\left[1-\frac{x^{2}}{5}\right]^{+}.
\end{equation}
The kernel estimators of $f$ and $\mathcal{H}$ are thus
\begin{equation}
\forall x \in \mathbb{R} \quad \widetilde{f}_{n}(x):=
\frac{1}{p} \sum_{i=1}^{p} \frac{1}{h_{i}} \kappa^{(E)}
\left(\frac{x-\lambda_{i}}{h_{i}}\right)=\frac{1}{p} \sum_{i=1}^{p}
\frac{1}{\lambda_{i} h} \kappa^{(E)}\left(\frac{x-\lambda_{i}}{\lambda_{i} h}\right)
\end{equation}
and
\begin{equation}
\mathcal{H}_{\tilde{f}_{n}}(x):=\frac{1}{p} \sum_{i=1}^{p} \frac{1}{h_{i}}
\mathcal{H}_{k}\left(\frac{x-\lambda_{i}}{h_{i}}\right)=\frac{1}{p} \sum_{i=1}^{p}
\frac{1}{\lambda_{i} h} \mathcal{H}_{k}\left(\frac{x-\lambda_{i}}
{\lambda_{i} h}\right)=\frac{1}{\pi} PV \int \frac{\widetilde{f}_{n}(t)}{x-t} d t,
\end{equation}
respectively. The feasible nonlinear shrinkage estimator is of rotation
equivariant form, where the elements of the diagonal matrix are
\begin{equation}
\forall i=1, \ldots, p \quad \widetilde{d}_{i}:=\frac{\lambda_{i}}
{\left[\pi \frac{p}{n} \lambda_{i} \widetilde{f}_{n}
\left(\lambda_{i}\right)\right]^{2}+\left[1-\frac{p}{n}-\pi
\frac{p}{n} \lambda_{i} \mathcal{H}_{\tilde{f}_{n}}\left(\lambda_{i}
\right)\right]^{2}}
\end{equation}
In other words, the feasible nonlinear shrinkage estimator is
\begin{equation}
\widetilde{\mathbf{S}}:=\sum_{i=1}^{p} \widetilde{d}_{i}
\mathbf{u}_{i} \mathbf{u}_{i}^{\prime}.
\end{equation}
References
----------
Ledoit, O. and Wolf, M. (2018).
Analytical nonlinear shrinkage of large-dimensional covariance matrices,
University of Zurich, Department of Economics, Working Paper (264).
"""
p, n = X.shape
S = np.cov(X)
sigma_tilde = _nonlinear_shrinkage_cov(S, n-1)
return sigma_tilde
def _nonlinear_shrinkage_cov(S, n):
"""
Shrink a sample covariance matrix with the analytic nonlinear shrinkage
formula of Ledoit and Wolf (2018). The code has been adapted from the
Matlab implementation provided by the authors in Appendix D.
Parameters
----------
S : numpy.ndarray, shape = (p, p)
The covariance matrix estimate based on a p by ``n`` sample.
n : int
The effective number of observations per feature.
Returns
-------
sigmatilde : numpy.ndarray, shape = (p, p)
The nonlinearly shrunk covariance matrix estimate.
Notes
-----
.. note::
Subtract the number of degrees of freedom lost due to prior estimations
from the number of observations per feature to compute ``n``.
E.g. if the feature has been de-meaned in the process of covariance matrix
estimation, subtract 1. If the covariance is based on residuals, subtract
the number of parameters of the estimator that produced the residuals.
Examples
--------
>>> np.random.seed(0)
>>> n = 13
>>> p = 6
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> S = np.cov(X.T)
>>> _nonlinear_shrinkage_cov(S,n-1)
array([[ 1.50231589e+00, -2.49140874e-01, 2.68050353e-01,
2.69052962e-01, 3.42958216e-01, -1.51487901e-02],
[-2.49140874e-01, 1.05011440e+00, -1.20681859e-03,
-1.25414579e-01, -1.81604754e-01, 4.38535891e-02],
[ 2.68050353e-01, -1.20681859e-03, 1.02797073e+00,
1.19235516e-01, 1.03335603e-01, 8.58533018e-02],
[ 2.69052962e-01, -1.25414579e-01, 1.19235516e-01,
1.03290514e+00, 2.18096913e-01, 5.63011351e-02],
[ 3.42958216e-01, -1.81604754e-01, 1.03335603e-01,
2.18096913e-01, 1.22086494e+00, 1.07255380e-01],
[-1.51487901e-02, 4.38535891e-02, 8.58533018e-02,
5.63011351e-02, 1.07255380e-01, 1.07710975e+00]])
>>> # This function can even handle singular covariance matrices.
>>> p = 14
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> S = np.cov(X.T)
>>> _nonlinear_shrinkage_cov(S,n-1)
array([[ 7.54515492e-01, -6.45326742e-02, -1.80320579e-01,
-3.57720108e-03, -7.97520403e-02, 1.36138395e-01,
-1.01345337e-02, 7.25279128e-02, -7.86780483e-02,
2.72372825e-02, 1.00706333e-02, -5.79499680e-02,
-1.25481898e-01, -1.48256429e-02],
[-6.45326742e-02, 8.44503245e-01, -1.24917494e-01,
-3.51829389e-02, 1.33441823e-01, 5.92079433e-02,
2.11138324e-02, -1.27753593e-03, 9.52252623e-02,
-2.11375517e-03, 9.64330095e-02, 5.23211671e-02,
-1.65536088e-01, 2.55397217e-02],
[-1.80320579e-01, -1.24917494e-01, 6.99399731e-01,
-4.04994408e-02, 3.55740241e-02, 1.57533721e-01,
-6.81649874e-02, 1.01763326e-01, -3.83272984e-02,
-5.46609875e-03, 8.38352683e-02, -8.09862188e-02,
-6.09294471e-02, 4.26805157e-02],
[-3.57720108e-03, -3.51829389e-02, -4.04994408e-02,
8.86179145e-01, -8.08767394e-02, 1.30951556e-02,
-1.72720919e-02, 1.50237335e-01, -1.15205858e-01,
-1.48730085e-01, 3.77860032e-02, 1.24465925e-02,
-5.68199278e-04, 2.94108399e-02],
[-7.97520403e-02, 1.33441823e-01, 3.55740241e-02,
-8.08767394e-02, 8.03855378e-01, 3.85564280e-02,
-1.73179369e-02, 8.22774366e-02, -2.03421197e-01,
-1.52509750e-02, -7.03293437e-02, -3.14963651e-02,
1.21756419e-01, 5.54656502e-03],
[ 1.36138395e-01, 5.92079433e-02, 1.57533721e-01,
1.30951556e-02, 3.85564280e-02, 8.07230306e-01,
-3.16636374e-02, 1.55275235e-03, 1.27215506e-01,
-7.58816222e-02, -1.37688973e-02, 1.67230701e-02,
1.09806724e-01, -5.06072120e-02],
[-1.01345337e-02, 2.11138324e-02, -6.81649874e-02,
-1.72720919e-02, -1.73179369e-02, -3.16636374e-02,
7.92866895e-01, 1.05036377e-01, 1.68442856e-01,
-1.01968600e-01, 1.76314684e-02, -1.06150243e-01,
3.90440121e-02, -2.52221857e-02],
[ 7.25279128e-02, -1.27753593e-03, 1.01763326e-01,
1.50237335e-01, 8.22774366e-02, 1.55275235e-03,
1.05036377e-01, 7.83954520e-01, -5.33212443e-03,
2.40305470e-01, -3.91748916e-02, 1.78156296e-01,
-4.31671138e-02, -4.71762192e-02],
[-7.86780483e-02, 9.52252623e-02, -3.83272984e-02,
-1.15205858e-01, -2.03421197e-01, 1.27215506e-01,
1.68442856e-01, -5.33212443e-03, 5.92364714e-01,
3.74973744e-02, -1.20092945e-02, 5.85976099e-02,
7.75487285e-02, 1.03957288e-01],
[ 2.72372825e-02, -2.11375517e-03, -5.46609875e-03,
-1.48730085e-01, -1.52509750e-02, -7.58816222e-02,
-1.01968600e-01, 2.40305470e-01, 3.74973744e-02,
7.16243320e-01, 8.94555209e-02, -1.44653465e-01,
7.22046121e-02, 9.86481306e-02],
[ 1.00706333e-02, 9.64330095e-02, 8.38352683e-02,
3.77860032e-02, -7.03293437e-02, -1.37688973e-02,
1.76314684e-02, -3.91748916e-02, -1.20092945e-02,
8.94555209e-02, 9.51436769e-01, 5.81230204e-02,
6.85744828e-02, -3.80840856e-02],
[-5.79499680e-02, 5.23211671e-02, -8.09862188e-02,
1.24465925e-02, -3.14963651e-02, 1.67230701e-02,
-1.06150243e-01, 1.78156296e-01, 5.85976099e-02,
-1.44653465e-01, 5.81230204e-02, 7.25021377e-01,
-1.19052381e-02, 2.75756708e-02],
[-1.25481898e-01, -1.65536088e-01, -6.09294471e-02,
-5.68199278e-04, 1.21756419e-01, 1.09806724e-01,
3.90440121e-02, -4.31671138e-02, 7.75487285e-02,
7.22046121e-02, 6.85744828e-02, -1.19052381e-02,
7.57919800e-01, -5.50198035e-02],
[-1.48256429e-02, 2.55397217e-02, 4.26805157e-02,
2.94108399e-02, 5.54656502e-03, -5.06072120e-02,
-2.52221857e-02, -4.71762192e-02, 1.03957288e-01,
9.86481306e-02, -3.80840856e-02, 2.75756708e-02,
-5.50198035e-02, 9.21548133e-01]])
References
----------
Ledoit, O. and Wolf, M. (2018).
Analytical nonlinear shrinkage of large-dimensional covariance matrices,
University of Zurich, Department of Economics, Working Paper (264).
"""
assert n >= 12, "Number of observations per feature should be at least 12."
p = S.shape[0]
# extract sample eigenvalues sorted in ascending order and eigenvectors.
lambd, u = np.linalg.eigh(S)
# compute analytical nonlinear shrinkage kernel formula.
lambd = lambd[np.maximum(0, p - n):]
L = np.tile(lambd, (np.minimum(p, n), 1)).T
h = n ** (-1 / 3)
# Equation(4.9)
H = h * L.T
x = (L - L.T) / H
ftilde = (3 / 4 / np.sqrt(5))
ftilde *= np.mean(np.maximum(1 - x ** 2 / 5, 0) / H, axis=1)
# Equation(4.7)
Hftemp = ((-3 / 10 / np.pi) * x
+ (3 / 4 / np.sqrt(5) / np.pi)
* (1 - x ** 2 / 5)
* np.log(np.abs((np.sqrt(5) - x) / (np.sqrt(5) + x))))
# Equation(4.8)
Hftemp[np.abs(x) == np.sqrt(5)] = ((-3 / 10 / np.pi)
* x[np.abs(x) == np.sqrt(5)])
Hftilde = np.mean(Hftemp / H, axis=1)
if p <= n:
dtilde = lambd / ((np.pi * (p / n) * lambd * ftilde) ** 2
+ (1 - (p / n)
- np.pi * (p / n) * lambd * Hftilde) ** 2)
# Equation(4.3)
else:
Hftilde0 =\
((1 / np.pi) * (3 / 10 / h ** 2 + 3 / 4 / np.sqrt(5) / h
* (1 - 1 / 5 / h ** 2)
* np.log((1 + np.sqrt(5) * h)
/ (1 - np.sqrt(5) * h))) * np.mean(1 / lambd))
# Equation(C.8)
dtilde0 = 1 / (np.pi * (p - n) / n * Hftilde0)
# Equation(C.5)
dtilde1 = \
lambd / (np.pi ** 2 * lambd ** 2 * (ftilde ** 2 + Hftilde ** 2))
# Equation(C.4)
dtilde = np.concatenate([dtilde0 * np.ones((p - n)), dtilde1])
sigmatilde = np.dot(np.dot(u, np.diag(dtilde)), u.T)
return sigmatilde
def _get_partitions(L):
"""
Get intraday partitions for NERIVE.
Parameters
----------
L : int > 1
The number of partitions.
Returns
-------
stp : list
The list of datetime.time objects.
"""
stp = [(datetime.datetime(2000, 1, 1, 9, 30)
+ datetime.timedelta(minutes=np.ceil(6.5/L*60)) * i).time()
for i in range(L)]
stp.append(datetime.time(16, 0))
return stp
[docs]def nerive(tick_series_list, stp=None, estimator=None, **kwargs):
r"""
The nonparametric eigenvalue-regularized integrated covariance matrix
estimator (NERIVE) of Lam and Feng (2018). This estimator is similar to
the :func:`~nercome` estimator extended into the hight frequency setting.
Parameters
----------
tick_series_list : list of pd.Series
Each pd.Series contains ticks of one asset with datetime index.
K : numpy.ndarray, default= ``None``
An array of sclales.
If ``None`` all scales :math:`i = 1, ..., M` are used, where M is
chosen :math:`M = n^{1/2}` acccording to Eqn (34) of Zhang (2006).
stp : array-like of datetime.time() objects, default = [9:30, 12:45, 16:00]
The split time points.
estimator : function, default = ``None``
An integrated covariance estimator taking ``tick_series_lists`` as
the first argument. If ``None`` the :func:`~msrc_pairwise` is used.
**kwargs : miscellaneous
Keyword arguments of the ``estimator``.
Returns
-------
out : numpy.ndarray, 2d
The NERIVE estimate of the integrated covariance matrix.
Notes
-----
The nonparametric eigenvalue-regularized integrated covariance matrix
estimator (NERIVE) proposed by Lam and Feng (2018) splits the sample into
$L$ partitions. The split points are denoted by
$$
0=\widetilde{\tau}_{0}<\widetilde{\tau}_{1}<\cdots<\widetilde{\tau}_{L}=T
$$
and the $l$th partition is given by $\left(\widetilde{\tau}_{l-1},
\widetilde{\tau}_{l}\right].$
The integrated covariance estimator for the $l$th partition is
\begin{equation}
\widehat{\mathbf{\Sigma}}_l=\mathbf{U}_{-l}
\operatorname{diag}\left(\mathbf{U}_{-l}'
\widetilde{\mathbf{\Sigma}}_l \mathbf{U}_{-l}\right) \mathbf{U}_{-l}'
\end{equation}
where $\mathbf{U}_{-l}$ is an orthogonal matrix depending on all
observations over the full interval $[0, T]$ except the $l$th partition.
The NERIVE estimator over the full interval $[0, T]$ is given by
\begin{equation}
\widehat{\mathbf{\Sigma}}=\sum_{l=1}^{L} \widehat{\mathbf{\Sigma}}_l=
\sum_{l=1}^{L} \mathbf{U}_{-l} \operatorname{diag}\left(\mathbf{U}_{-l}'
\widetilde{\mathbf{\Sigma}}_l \mathbf{U}_{-l}\right) \mathbf{U}_{-l}'.
\end{equation}
$\widetilde{\mathbf{\Sigma}}$ is an integrated covariance estimator that
corrects for asynchronicity and microstructure noise, e.g., one of
:mod:`hf`. Lam and Feng (2018) choose the TSRC for the sake of tractablility
in the proofs. Importantly, NERIVE does not assume
i.i.d. observations but weak dependence between the log-price process and
the microstructure noise process within partition $l$, and weak serial
dependence of microstructure noise vectors, given $\mathcal{F}_{-l}$.
Similar to NERCOME, NERIVE allows for the presence of pervasive factors as
long as they persist between refresh times.
.. warning::
NERIVE splits the data into smaller subsamples. Estimator
parameters that depend on the sample size must be adjusted.
Further, the price process must be preprocessed to have zero mean
return over the **full** sample.
References
----------
Lam, C. and Feng, P. (2018). A nonparametric eigenvalue-regularized
integrated covariance matrix estimator for asset return data,
Journal of Econometrics 206(1): 226–257.
"""
# TODO extend to multiple days, each partition should then be
# one day and the cov for eigenmatrix is average of individual day covs.
last_series_date = None
for series in tick_series_list:
assert series.index[0].date() == series.index[-1].date(),\
"""All tick times must be contained within one day. NERIVE is an
intraday estimator."""
if last_series_date is not None:
assert series.index[0].date() == last_series_date,\
"""The date of tick times of all assets must be equal."""
last_series_date = series.index[0].date()
if estimator is None:
estimator = hf.msrc_pairwise
if stp is None:
stp = _get_partitions(4)
L = len(stp) - 1
Sigma_hat_list = []
for j in range(L):
ticks_j = [x.between_time(stp[j], stp[j+1], True, True)
for x in tick_series_list]
ticks_notj = [x.between_time(stp[j+1], stp[j], False, False)
for x in tick_series_list]
Lambda, P_not_j = np.linalg.eigh(estimator(ticks_notj, **kwargs))
Sigma_tilde = estimator(ticks_j, **kwargs)
D = np.diag(np.diag(P_not_j.T @ Sigma_tilde @ P_not_j))
Sigma_hat = P_not_j @ D @ P_not_j.T
Sigma_hat_list.append(Sigma_hat)
return np.mean(Sigma_hat_list, axis=0)
[docs]def nercome(X, m=None, M=50):
r"""
The nonparametric eigenvalue-regularized covariance matrix estimator
(NERCOME) of Lam (2016).
Parameters
----------
X : numpy.ndarray, shape = (p, n)
A 2d array of log-returns (n observations of p assets).
m : int, default = ``None``
The size of the random split with which the eigenvalues
are computed. If ``None`` the estimator searches over values
suggested by Lam (2016) in Equation (4.8) and selects the
best according to Equation (4.7).
M : int, default = 50
The number of permutations. Lam (2016) suggests 50.
Returns
-------
opt_Sigma_hat : numpy.ndarray, shape = (p, p)
The NERCOME covariance matrix estimate.
Examples
--------
>>> np.random.seed(0)
>>> n = 13
>>> p = 5
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> cov = nercome(X.T, m=5, M=10)
>>> cov
array([[ 1.34226722, 0.09693429, 0.00233125, 0.17717658, -0.01643898],
[ 0.09693429, 1.0508423 , 0.10112215, -0.22908987, -0.04914651],
[ 0.00233125, 0.10112215, 1.0731665 , -0.02959628, 0.38652859],
[ 0.17717658, -0.22908987, -0.02959628, 1.10753766, 0.1807373 ],
[-0.01643898, -0.04914651, 0.38652859, 0.1807373 , 0.88832791]])
Notes
-----
A very different approach to the analytic formulas of nonlinear shrinkage
is pursued by Abadir et al 2014.
These authors propose a nonparametric estimator based
on a sample splitting scheme. They split the data into two pieces and
exploit the independence of observations across the splits to regularize
the eigenvalues. Lam (2016) builds on their results and proposes a
nonparametric estimator that is asymptotically optimal even if the
population covariance matrix $\mathbf{\Sigma}$ has a factor structure.
In the case of low-rank strong factor models, the assumption that each
observation can be written as $\mathbf{x}_{t}
=\mathbf{\Sigma}^{1 / 2} \mathbf{z}_{t}$ for $t=1, \ldots, n,$
where each $\mathbf{z}_{t}$ is a $p \times 1$ vector of independent and
identically distributed random variables $z_{i t}$, for $i=1, \ldots, p,$
with zero-mean and unit variance, is violated since the covariance matrix
is singular and its Cholesky decomposition does not exist.
Both :func:`linear_shrinkage` and :func:`nonlinear_shrinkage` are build on
this assumption are no longer optimal if it is not fulfilled. The proposed
nonparametric eigenvalue-regularized covariance matrix estimator (NERCOME)
starts by splitting the data into two pieces of size $n_1$ and $n_2 = n - n_1$.
It is assumed that the observations are i.i.d with finite fourth moments such
that the statistics computed in the different splits are likewise
independent of each other. The sample covariance matrix of the first
partition is defined as $\mathbf{S}_{n_1}:=
\mathbf{X}_{n_1}\mathbf{X}_{n_1}'/n_1$. Its spectral decomposition
is given by $\mathbf{S}_{n_1}=\mathbf{U}_{n_1}
\mathbf{\Lambda}_{n_1} \mathbf{U}_{n_1}^{\prime},$ where
$\mathbf{\Lambda}_{n_1}$ is a diagonal matrix, whose elements are the
eigenvalues $\mathbf{\lambda}_{n_1}=\left(\lambda_{n_1, 1}, \ldots,
\lambda_{n_1, p}\right)$ and an orthogonal matrix $\mathbf{U}_{n_1}$,
whose columns $\left[\mathbf{u}_{n_1, 1} \ldots
\mathbf{u}_{n_1, p}\right]$ are the corresponding eigenvectors.
Analogously, the sample covariance matrix of the second partition is
defined by $\mathbf{S}_{n_2}:=
\mathbf{X}_{n_2}\mathbf{X}_{n_2}'/n_2$. Theorem 1 of
Lam (2016) shows that
\begin{equation}
\widetilde{\mathbf{d}}_{n_1}^{(\text{NERCOME})}=
\operatorname{diag}( \mathbf{U}_{n_1}^{\prime} \mathbf{S}_{n_2}
\mathbf{U}_{n_1})
\end{equation}
is asymptotically the same as the finite-sample optimal rotation
equivariant $\mathbf{d}_{n_1}^{*} = \mathbf{U}_{n_1}^{\prime}
\mathbf{\Sigma} \mathbf{U}_{n_1}$
based on the section $n_1$. The proposed estimator is thus of the rotation
equivariant form, where the elements of the diagonal matrix are chosen
according to $\widetilde{\mathbf{d}}_{n_1}^{(\text{NERCOME})}$.
In other words the estimator is given by
\begin{equation}
\widetilde{\mathbf{S}}_{ n_1}^{(\text{NERCOME})}:=
\sum_{i=1}^{p}\widetilde{\mathbf{d}}_{n_1}^{(\text{NERCOME})} \cdot
\mathbf{u}_{n_1, i} \mathbf{u}_{n_1, i}^{\prime}
\end{equation}
The author shows that this estimator is asymptotically optimal with
respect to the Frobenius loss even under factor structure. However, it uses
the sample data inefficiently since only one section is utilized for the
calculation of each component. The natural extension is to permute the data
and bisect it anew. With these sections an estimate is computed according
to $\widetilde{\mathbf{S}}_{ n_1}^{(\text{NERCOME})}$. This is done $M$
times and the covariance matrix estimates are averaged:
\begin{equation}
\widetilde{\mathbf{S}}_{n_1, M}^{(\text{NERCOME})}:=\frac{1}{M}
\sum_{j=1}^{M}\widetilde{\mathbf{S}}_{n_1, j}^{(\text{NERCOME})}.
\end{equation}
The estimator depends on two tuning parameters, $M$ and $n_1$. Higher $M$
give more accurate results but the computational cost grows as well. The
author suggests that more than 50 iterations are generally not needed for
satisfactory results. $n_1$ is subject to regularity conditions. The author
proposes to search over the contenders
\begin{equation}
n_1=\left[2 n^{1 / 2}, 0.2 n, 0.4 n, 0.6 n, 0.8 n, n-2.5 n^{1 / 2},
n-1.5 n^{1 / 2}\right]
\end{equation}
and select the one that minimizes the following criterion inspired by
Bickel (2008)
\begin{equation}
g(n_1)=\left\|\frac{1}{M} \sum_{j=1}^{M}
\left(\widetilde{\mathbf{S}}_{n_1, j}^{(\text{NERCOME})}
-\mathbf{S}_{n_2, j}\right)\right\|_{F}^{2}.
\end{equation}
References
----------
Abadir, K. M., Distaso, W. and Zikeˇs, F. (2014).
Design-free estimation of variance matrices,
Journal of Econometrics 181(2): 165–180.
Bickel, P. J. and Levina, E. (2008).
Regularized estimation of large covariance matrices,
The Annals of Statistics 36(1): 199–227.
Lam, C. (2016).
Nonparametric eigenvalue-regularized precision or covariance matrix estimator,
The Annals of Statistics 44(3): 928–953.
"""
p, n = X.shape
if m is None:
m_list = [int(2 * n ** 0.5), int(0.2 * n), int(0.4 * n), int(0.6 * n),
int(0.8 * n), int(n - 2.5*n ** 0.5), int(n - 1.5 * n ** 0.5)]
Sigmas = [_nercome(X, m, M) for m in m_list]
idx = _optimal_nere(Sigmas)
opt_Sigma_hat = Sigmas[idx][0]
else:
opt_Sigma_hat = _nercome(X, m, M)[0]
return opt_Sigma_hat
def _nercome(X, m, M):
"""
Comute the NERCOME estimator.
Parameters
----------
X : numpy.ndarray, shape = (p, n)
A 2d array of log-returns (n observations of p assets).
m : int
The number of observations in each random sample.
M : int
The number of permutations.
Returns
-------
(Sigma_hat, Sigma_tilde) : tuple
Sigma_hat is the NERCOME estimate of the covariance matrix.
Sigma_tilde is the averaged (over the M permutations) sample covariance
matrix of the random split samples of size m, which is needed for
:func:`~_optimal_nere'.
"""
p, n = X.shape
Sigma_hat_sum = np.zeros((p, p))
Sigma_tilde_sum = np.zeros((p, p))
for j in range(M):
idx_m = np.random.randint(0, n, m)
mask = np.ones(n, dtype=np.int64)
mask[idx_m] = int(0)
Lambda, P_1 = np.linalg.eigh(np.cov(X[:, mask]))
Sigma_tilde = np.cov(X[:, idx_m])
D = np.diag(np.diag(P_1.T @ Sigma_tilde @ P_1))
Sigma_hat = P_1 @ D @ P_1.T
Sigma_hat_sum += Sigma_hat
Sigma_tilde_sum += Sigma_tilde
Sigma_hat = Sigma_hat_sum/M
Sigma_tilde = Sigma_tilde_sum/M
return (Sigma_hat, Sigma_tilde)
def _optimal_nere(Sigmas):
"""
Determine the optimal nonparametric eigenvalue regularized estimator
per Equation (4.7) of Lam (2016).
Parameters
----------
Sigmas : list of tuples
Each element of the list is a tuple with Sigma_hat as the 0th
element and Sigma_tilde as the 1st element.
Returns
-------
idx: int
The index of the best estimator.
"""
norms = [np.linalg.norm(x[0] - x[1], 'fro')**2 for x in Sigmas]
idx_best = np.argmin(norms)
return idx_best
[docs]@numba.njit
def to_corr(cov):
"""Convert a covariance matrix to a correlation matrix.
Parameters
----------
cov : numpy.ndarray, 2d, float
A covariance matrix.
Returns
-------
out : numpy.ndarray, 2d
A correlation matrix
Examples
--------
>>> cov = np.array([[2., 1.],[1., 2.]])
>>> to_corr(cov)
array([[1. , 0.5],
[0.5, 1. ]])
"""
L = np.diag(1./np.sqrt(np.diag(cov)))
return L @ cov @ L.T