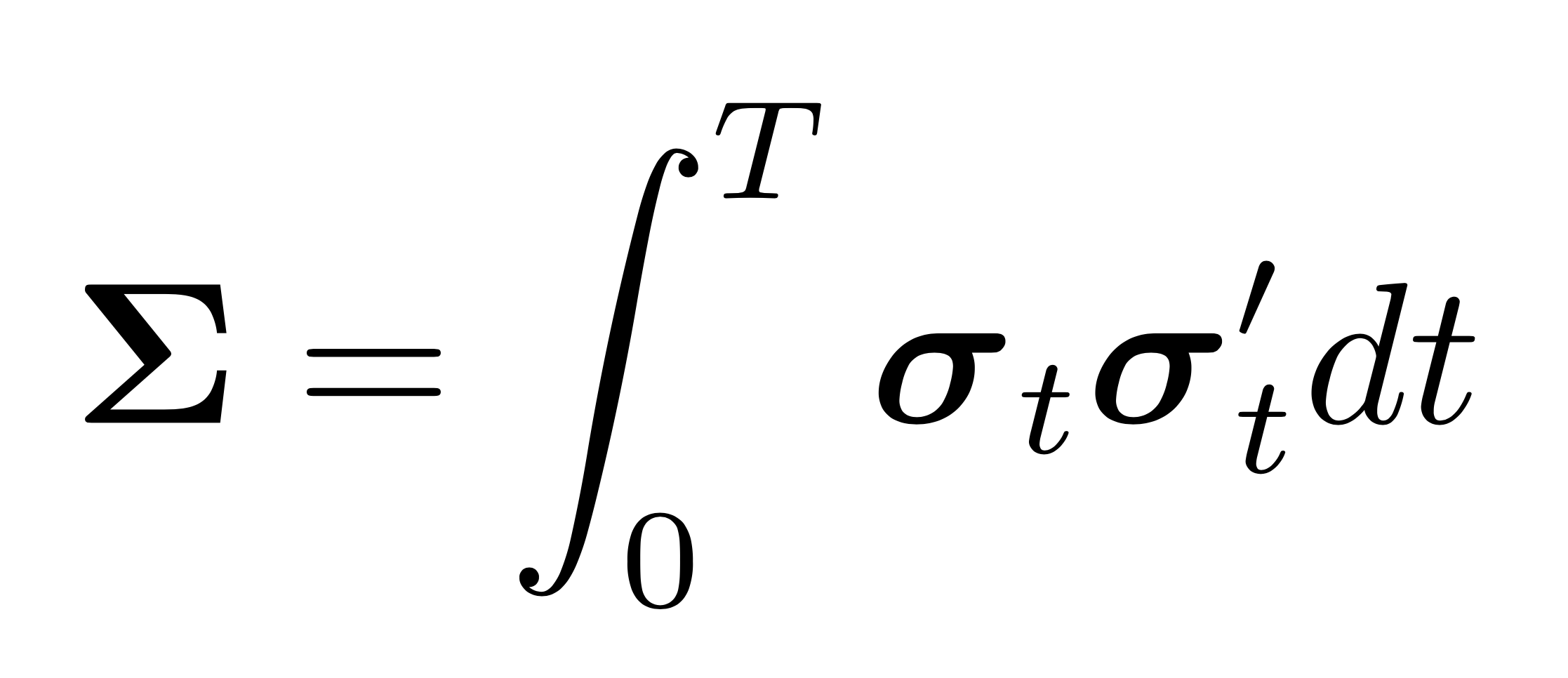linear_shrinkage

hd.linear_shrinkage(X)

The linear shrinkage estimator of Ledoit and Wolf (2004). The observations need to be synchronized and i.i.d.

Parameters

Xnumpy.ndarray, shape = (p, n)

A sample of synchronized log-returns.

Returns

shrunk_covnumpy.ndarray

The linearly shrunk covariance matrix.

Notes

The most ubiquitous estimator of the rotation equivariant type is perhaps the linear shrinkage estimator of Ledoit and Wolf (2004). These authors propose a weighted average of the sample covariance matrix and the identity (or some other highly structured) matrix that is scaled such that the trace remains the same. The weight, or shrinkage intensity, \(\rho\) is chosen such that the squared Frobenius loss is minimized by inducing bias but reducing variance. In Theorem 1, the authors show that the optimal \(\rho\) is given by \begin{equation} \rho=\beta^{2} /\left(\alpha^{2}+\beta^{2}\right)=\beta^{2} / \delta^{2}, \end{equation} where \(\mu=\operatorname{tr}(\mathbf{\Sigma})/p\), \(\alpha^{2}= \|\mathbf{\Sigma}-\mu \mathbf{I}_p\|_{F}^{2}\), \(\beta^{2}= E\left[\|\mathbf{S}-\mathbf{\Sigma}\|_{F}^{2}\right]\), and \(\delta^{2}=E\left[\|\mathbf{S}-\mu \mathbf{I}_p\|_{F}^{2}\right]\). \(\beta^{2} / \delta^{2}\) can be interpreted as a normalized measure of the error of the sample covariance matrix. Shrinking the covariance matrix towards the \(\mu\)-scaled identity matrix has the effect of pulling the eigenvalues towards \(\mu\). This reduces eigenvalue dispersion. In other words, the elements of the diagonal matrix in the rotation equivariant form are chosen as \begin{equation} \widehat{\mathbf{\delta}}^{(l, o)}:=\left(\widehat{d}_{1}^{(l, o)}, \ldots, \widehat{d}_{p}^{(l, o)}\right)=\left(\rho \mu+(1-\rho) \lambda_{1}, \ldots, \rho \mu+(1-\rho) \lambda_{p}\right). \end{equation} In the current form it is still an oracle estimator since it depends on ] unobservable quantities. To make it a feasible estimator, these quantities have to be estimated. To this end, define the grand mean as \begin{equation} \label{eqn: grand mean} \bar{\lambda}:=\frac{1}{p} \sum_{i=1}^{p} \lambda_{i}, \end{equation} The estimator for \(\rho\) is given by \begin{equation} \widehat{\rho} : = \frac{b^{2}}{d^{2}}, \end{equation} where \(d^{2}=\left\|\mathbf{S}-\bar{\lambda} \mathbf{I}_{p} \right\|_{F}^{2}\) and \(b^{2}=\min \left(\bar{b}^{2}, d^{2}\right)\) with \(\bar{b}^{2}=\frac{1}{n^{2}} \sum_{k=1}^{n}\left\|\mathbf{x}_{k} \left(\mathbf{x}_{k}\right)^{\prime}-\mathbf{S}\right\|_{F}^{2}\), where \(\mathbf{x}_{k}\) denotes the \(k\)th column of the observation matrix \(\mathbf{X}\) for \(k=1, \ldots, n\). In order for this estimator to be consistent, the assumption that \(\mathbf{X}\) is i.i.d with finite fourth moments must be satisfied. The feasible linear shrinkage estimator is then of form rotation equivatiant form with the elements of the diagonal chosen as \begin{equation} \widehat{\mathbf{\delta}}^{(l)}:=\left(\widehat{d}_{{1}}^{(l)}, \ldots, \widehat{d}_{p}^{(l)}\right)=\left( \widehat{\rho} \bar{\lambda}+ (1- \widehat{\rho}) \lambda_{1}, \ldots, \widehat{\rho} \bar{\lambda}+ (1- \widehat{\rho}) \lambda_{p}\right). \end{equation} Hence, the linear shrinkage estimator is given by \begin{equation} \widehat{\mathbf{S}}:=\sum_{i=1}^{p} \widehat{d}_{i}^{(l)} \mathbf{u}_{i} \mathbf{u}_{i}^{\prime} \end{equation} The result is a biased but well-conditioned covariance matrix estimate.

References

Ledoit, O. and Wolf, M. (2004). A well-conditioned estimator for large-dimensional covariance matrices, Journal of Multivariate Analysis 88(2): 365–411.

Examples

>>> np.random.seed(0)
>>> n = 5
>>> p = 5
>>> X = np.random.multivariate_normal(np.zeros(p), np.eye(p), n)
>>> cov = linear_shrinkage(X.T)
>>> cov
array([[1.1996234, 0.       , 0.       , 0.       , 0.       ],
       [0.       , 1.1996234, 0.       , 0.       , 0.       ],
       [0.       , 0.       , 1.1996234, 0.       , 0.       ],
       [0.       , 0.       , 0.       , 1.1996234, 0.       ],
       [0.       , 0.       , 0.       , 0.       , 1.1996234]])