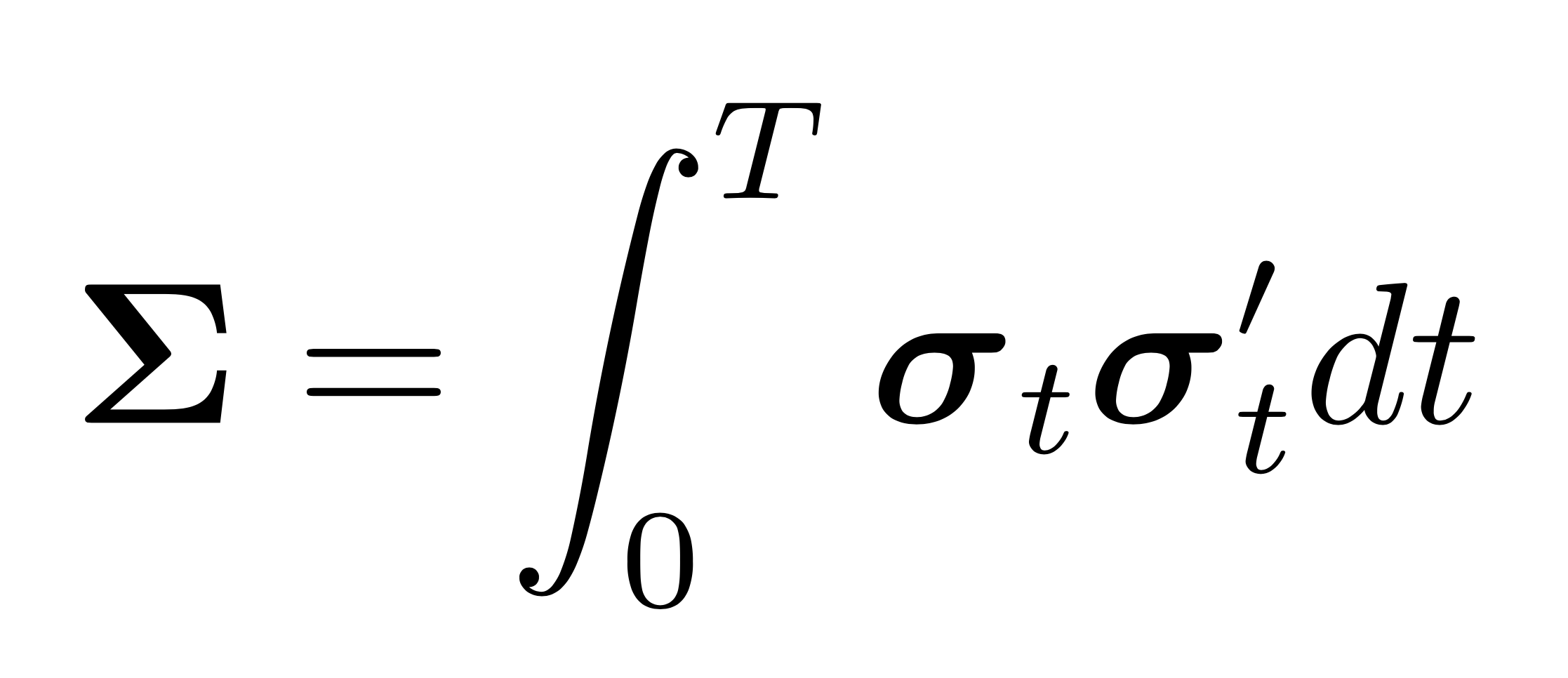tsrc

hf.tsrc(tick_series_list, J=1, K=None)

The two-scales realized volatility (TSRV) of Zhang et al. (2005). It is extentended to handle multiple dimension according to Zhang (2011). msrc() has better convergence rate and is thus prefrerred.

Parameters

tick_series_listlist of pd.Series

Each pd.Series contains tick-log-prices of one asset with datetime index.

Kint, default = int(n**(2/3))

long scale, default = int(n**(2/3)) as per Zhang (2005)

Jint, default = 1

short scale

Returns

outnumpy.ndarray

The TSRV estimate.

Notes

The two-scales realized volatility (TSRV) estimator is defined as

\begin{equation} \widehat{\langle X^{(j)}, X^{(j)}\rangle}^{(\mathrm{TSRV})}_{T}= \left[Y^{(j)}, Y^{(j)}\right]_{T}^{(K)}-\frac{\bar{n}_{K}}{\bar{n}_{J}} \left[Y^{(j)}, Y^{(j)}\right]_{T}^{(J)}, \end{equation} where \begin{equation} \left[Y^{(j)}, Y^{(j)}\right]_{T}^{(K)}=\frac{1}{K} \sum_{i=K}^{n}\left(Y_{\tau_{i}^{(j)}}^{(j)}- Y_{\tau_{i-K}^{(j)}}^{(j)}\right)^2, \end{equation} with \(K\) being a positive integer usually chosen much larger than 1 and \(\bar{n}_{K}=\left(n-K+1\right)/K\) and \(\bar{n}_{J}=\left(n- J+1\right)/J\). If \(K\) is chosen on the order of\(K=\mathcal{O}\left(n^{2 / 3}\right)\) this estimator is asymptotically unbiased, consistent, asymptotically normal distributed and converges at rate \(n^{-1 / 6}\).

Zhang (2011) proposes the (multivariate) two scales realized covariance (TSCV) estimator based on previous-tick times of asset \(k\) and \(l\), which simultaneously corrects for the bias due to asynchronicity and the bias due to microstructure noise. Previous-tick times may be computed via refresh_time().

The TSCV estimator is defined as \begin{equation} \widehat{\langle X^{(k)},X^{(l)}\rangle}_{T}^{(TSCV)}=c\left(\left[Y^{(k)}, Y^{(l)}\right]_{T}^{(K)}-\frac{\bar{n}_{K}}{\bar{n}_{J}}\left[Y^{(k)}, Y^{(l)}\right]_{T}^{(J)}\right), \end{equation} where \begin{equation} \left[Y^{(k)}, Y^{(l)}\right]_{T}^{(K)}=\frac{1}{K} \sum_{i=K}^{\tilde{n}}\left(Y^{(k)}_{\tau^{(k)}_{i}}-Y^{(k)}_{\tau^{(k)}_{i-K}} \right)\left(Y^{(l)}_{\tau^{(l)}_{i}}-Y^{(l)}_{\tau^{(l)}_{i-K}}\right) \end{equation} \(c=1+o_{p}\left(\tilde{n}^{-1 / 6}\right)\) is a small sample correction. \(K\) is again a positive integer usually chosen much larger than 1 and \(\bar{n}_{K}=\left(\tilde{n}- K+1\right) / K\) and \(\bar{n}_{J}= \left(\tilde{n}- J+1\right) / J\). The author shows that if \(K=\mathcal{O}\left((n^{(k)}+n^{(l)})^{2/3}\right)\) this estimator is asymptotically unbiased, consistent, asymptotically normal distributed and converges at rate \(\tilde{n}^{-1 / 6}\).

Note

Use msrc() since it has better converges rate.

References

Zhang, L., Mykland, P. A. and Ait-Sahalia, Y. (2005). A tale of two time scales: Determining integrated volatility with noisy high-frequency data, Journal of the American Statistical Association 100(472): 1394–1411.

Zhang, L. (2011). Estimating covariation: Epps effect, microstructure noise, Journal of Econometrics 160.

Examples

>>> np.random.seed(0)
>>> n = 200000
>>> returns = np.random.multivariate_normal([0, 0], [[1, 0.5],[0.5, 1]], n)/n**0.5
>>> prices = 100*np.exp(returns.cumsum(axis=0))
>>> # add Gaussian microstructure noise
>>> noise = 10*np.random.normal(0, 1, n*2).reshape(-1, 2)*np.sqrt(1/n**0.5)
>>> prices += noise
>>> # sample n/2 (non-synchronous) observations of each tick series
>>> series_a = pd.Series(prices[:, 0]).sample(int(n/2)).sort_index()
>>> series_b = pd.Series(prices[:, 1]).sample(int(n/2)).sort_index()
>>> # take logs
>>> series_a = np.log(series_a)
>>> series_b = np.log(series_b)
>>> icov_c = tsrc([series_a, series_b])
>>> # This is the unbiased,  corrected integrated covariance matrix estimate.
>>> np.round(icov_c, 3)
array([[0.995, 0.361],
       [0.361, 0.977]])