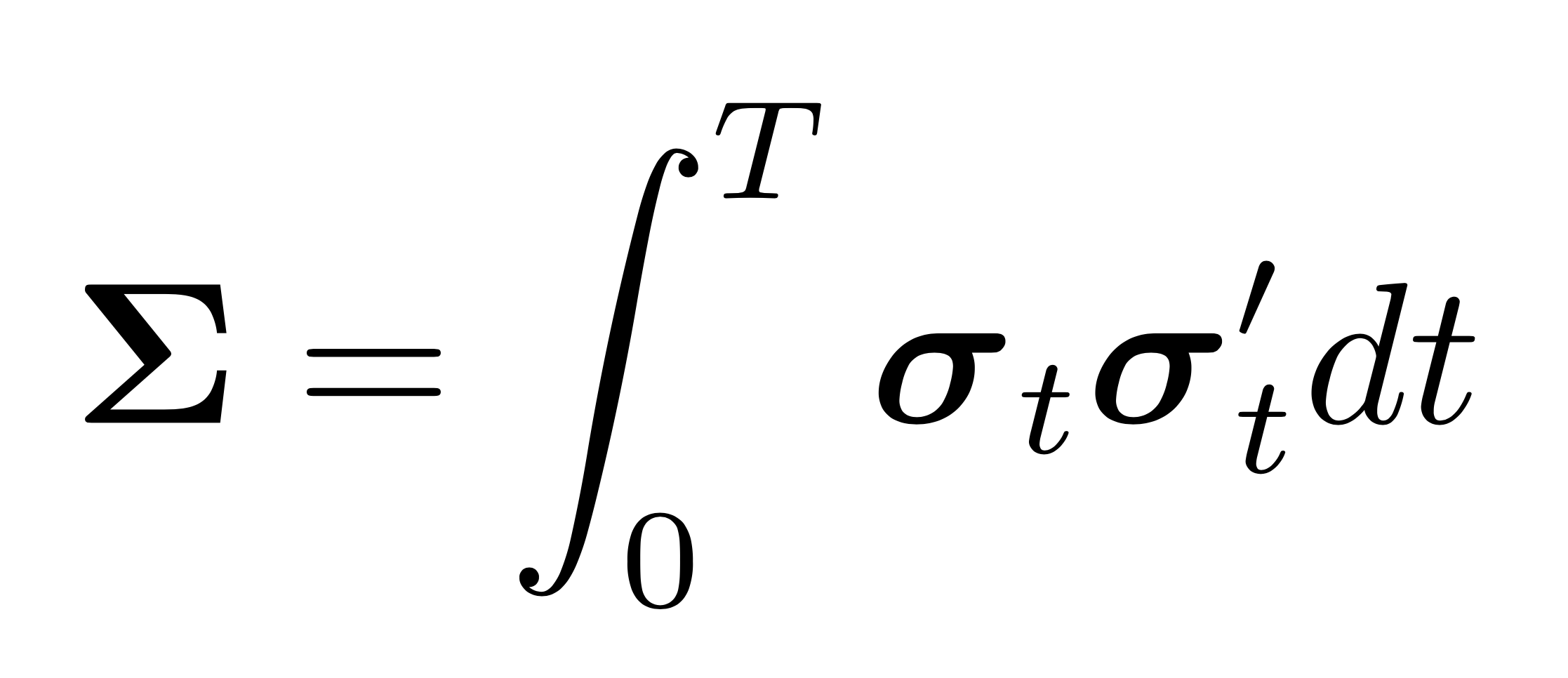marchenko_pastur

loss.marchenko_pastur(x, c, sigma_sq)

The Marchenko-Pastur distribution. This is the pdf of eigenvalues of a sample covariance matrix estimate of the true covariance matrix, which is a``sigma_sq`` scaled identity matrix. It depends on the concentration ratio c, which is the ratio of the dimension divided by the number of observations.

Parameters

xfloat

The value of the sample eigenvalue.

cfloat

The concentration ratio. \(c=p/n\).

sigma_sqfloat

The value of population eigenvalues.

Returns

pfloat

The value of the Marchenko-Pastur distribution at the sample eigenvalue x.

Notes

The Marchenko-Pastur law states that the limiting spectrum of the sample covariance matrix \(S = {X 'X}/n\) of independent and identically distributed \(p\)-dimensional random vectors \(\mathbf{X}=\left(x_{1}, \ldots, x_{n}\right)\) with mean \(\mathbf{0}\) and covariance matrix \(\mathbf{\Sigma}=\sigma^{2} \mathbf{I}_{p}\), has density \begin{equation} f_{c}(x)=\left\{\begin{array}{ll} \frac{1}{2 \pi x c \sigma^{2}} \sqrt{(b-x)(x-a)}, & a \leq x \leq b \ 0, & \text { otherwise, } \end{array}\right. \end{equation} where the smallest and the largest eigenvalues are given by \(a=\sigma^{2}(1-\sqrt{c})^{2}\) and \(b=\sigma^{2}(1+\sqrt{c})^{2}\), respectively, as \(p, n \rightarrow \infty\) with \(p / n \rightarrow c>0\).

References

Marchenko, V. A. and Pastur, L. A. (1967). Distribution of eigenvalues for some sets of random matrices, Matematicheskii Sbornik 114(4): 507–536.